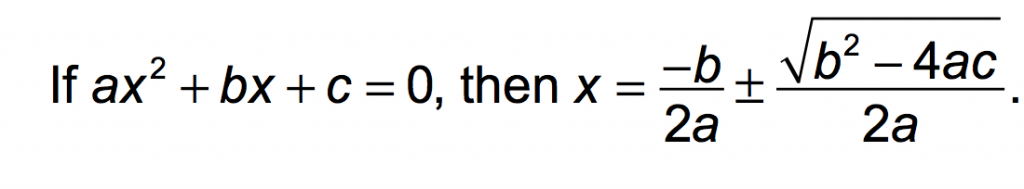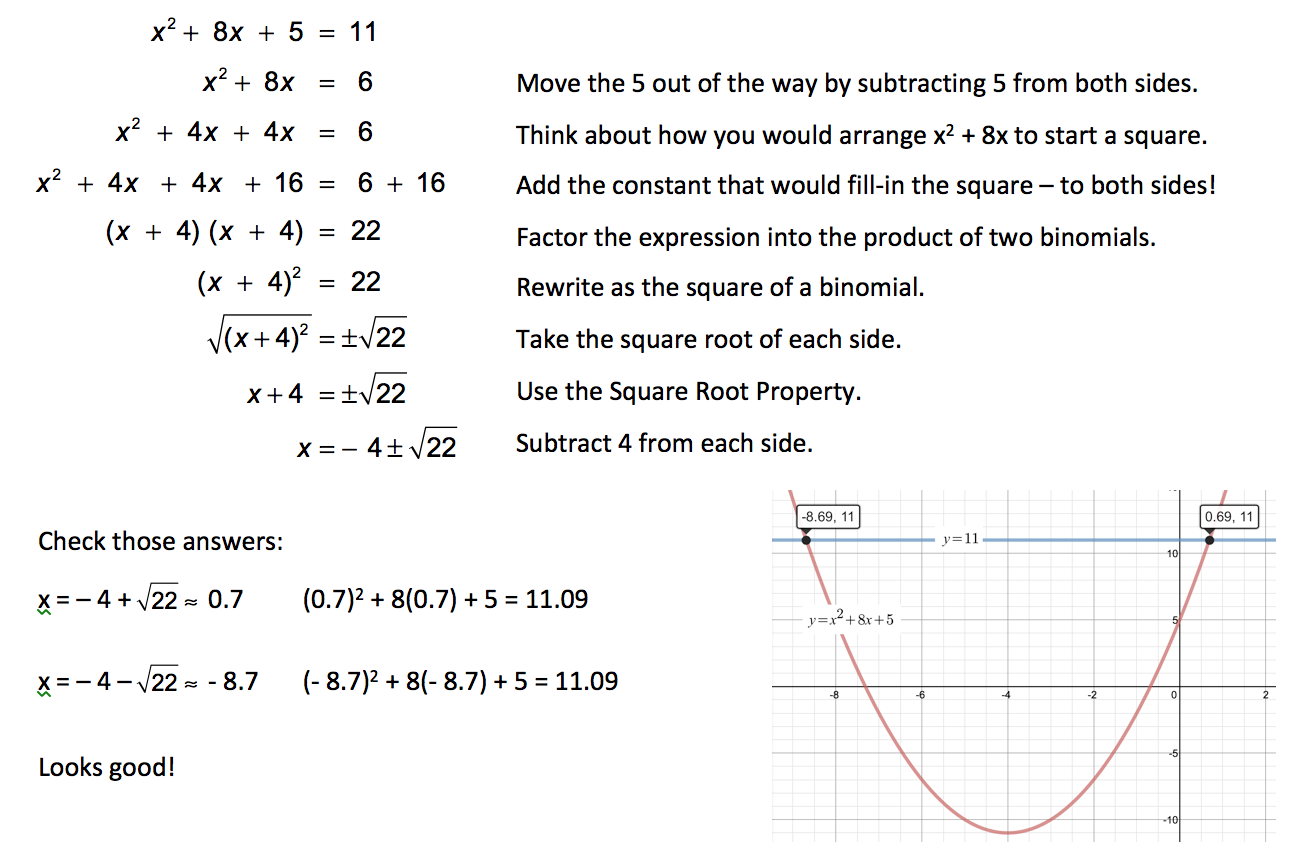
What would you do if you were asked to solve for x?                  x² + 8x + 5 = 11

You would probably set the quadratic equal to zero and try to factor, right?

Can you factor this quadratic trinomial?             x² + 8x – 6 = 0           Sadly, no.

 

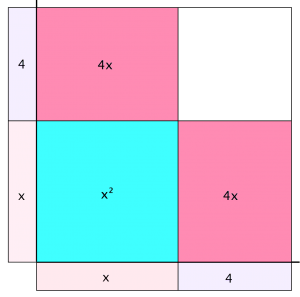
There’s another technique for solving quadratic equations, called Completing the Square. If you can create a perfect square trinomial, you can replace it with the square of the binomial and take the square root. That’s the plan; let’s see how it’s done.

We have   x² + 8x + 5 = 11.   Ignore the constants for now, we can deal with those later.

To make a square, we have to break the 8x evenly in 2 parts. When we do that, we see that the factors must be (x + 4)(x + 4).

What do we need as a constant? The missing corner is 4 x 4, so we need 16.

Let’s look at it with algebra.

 

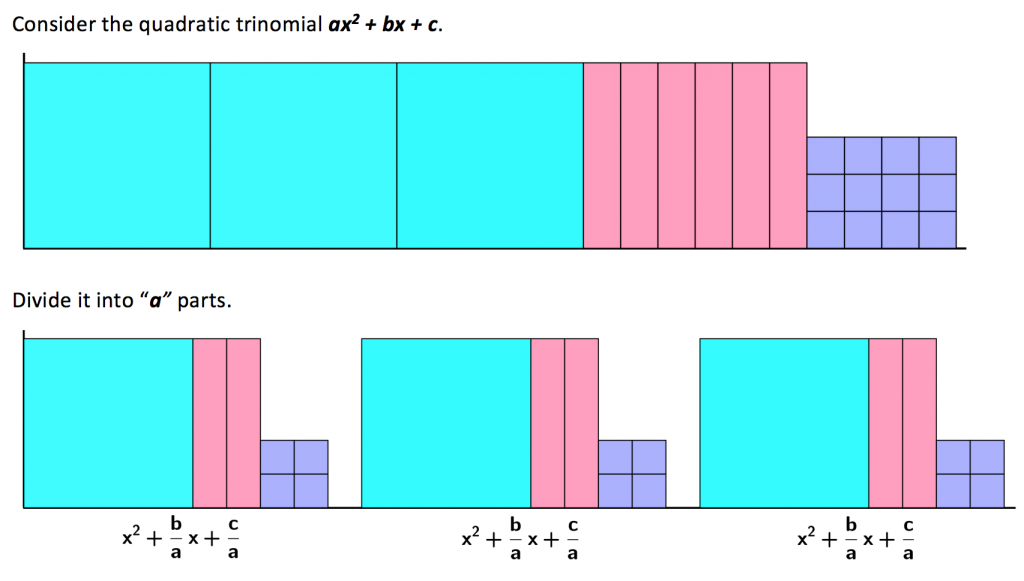
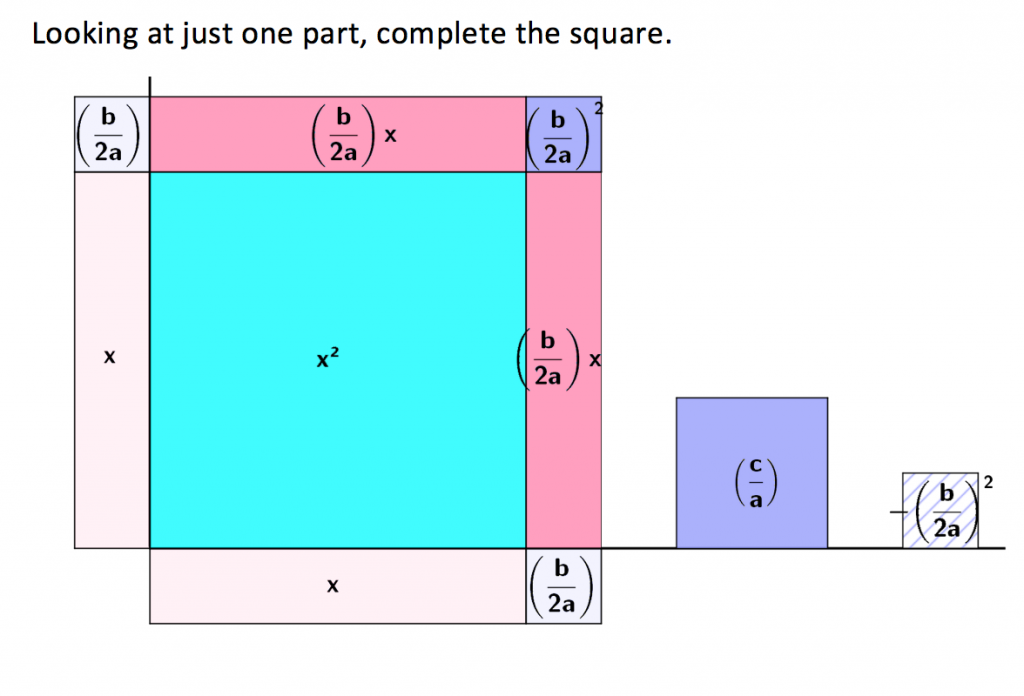
If we can generalize this technique to any quadratic equation, we can create a formula to use to solve for x, every time.

Hot dog!

  

 

 

 

 

 

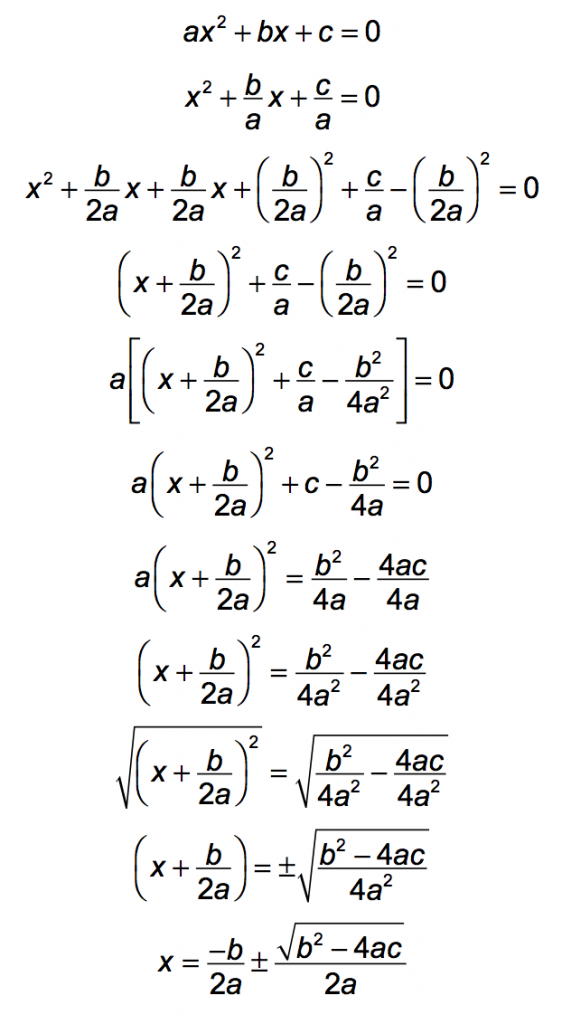
After lots of algebra…

 

 

 

 

 

We have the Quadratic Formula: