This is a quick preview, I will expand upon it when I can.

Here is the outline of another approach to the beginning of Geometry, where each major step can be observed through software or manipulatives, since they are visually obvious, or demonstrated through coordinate geometry. Some must be postulates, others can then be proven.

1. Translations, Rotations, and Reflections are isometries, that is, they maintain size and shape.

2. Congruent figures are defined as the result of isometries.

3. CPCTC, including altitudes.

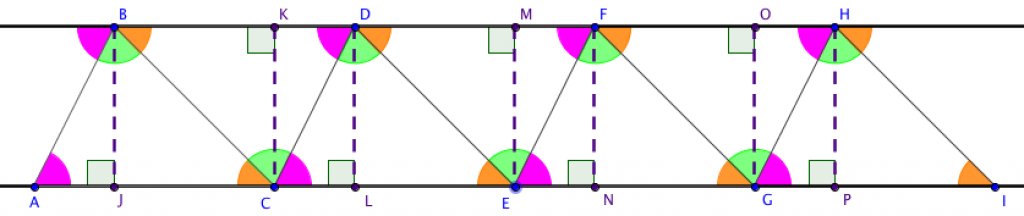
4. Put [1] – [3] together. Each triangle in the figure below is a rotation about the midpoint of the adjacent side.

5. Lines equidistant at 2 places are equidistant everywhere.

6. Equidistant lines are defined as parallel.

7. Angle pairs formed by parallel lies intersected by a transversal can be explored, and their relationships proven, by constructing and transforming appropriate figures.

OK, so that’s my thinking. What do you think? Please let me know!