A week or so ago, the folks at MathMunch posted a piece about rhombic dodecs. Well, I love solid geometry, and it tied into my earlier study of honeycombs, so I was quickly hooked! I revised the nets they provided using GeoGebra, so I could locate the center of each rhombus to attach a magnet. I printed them on my snazzy custom-printed card stock, and started to build!

As you see, they fit together (less manufacturing defects) in one layer; you could say that they tessellate. But they are even cooler than that! They also fit together in space – they hyper-tesselate! (I made that up…)

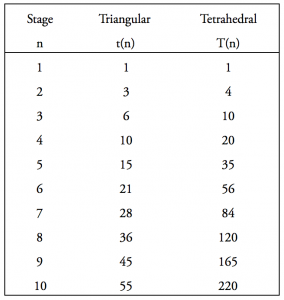Then I started thinking about how they fit together. In a single layer, they can be arranged in triangular numbers. If we build them up in layers, this is what we get:

So, the t(n) column keeps a running total of the n column, and the T(n) column keeps a running total of the t(n) column.

This is how it might be represented, but I may be butchering the notation. If anyone can steer me toward an accessible academic treatment of my observations, I’d appreciate it.

I think this would make a nice lesson if each student in a class made rhombic dodecagon. Then, first in small groups, and then in a larger group, they could experiment with how the solids could fit together. It would be cool for kids to discover what I discovered – or something totally different! And you don’t need snazzy paper or magnets – that’s just me – manila file folders work just fine!

OK, time to work on my day job; my next post will be about the “solid angles” meeting at each intersection of rhombic dodecs. Thanks for the inspiration, Justin, Anna, and Paul!