There is a very old fable about a crow and a partially-filled pitcher of water. Here is a modern retelling of the story, taken from an advertisement for Birla Sun Life, an Indian investment company.

Today you get to play the part of the crow! Brainstorm a few ideas to get to the water – you are a thirsty crow!

.

.

.

.

Here’s what the crow decided to do:

.

.

.

.

How many pebbles does the crow need?

.

.

Activity:

Gather your supplies: a cylindrical jar or glass filled about half-way, six stones, a ruler, a post-it for noting water heights, a GeoGebra Spreadsheet.

1. Measure the height of the jar and subtract 2 centimeters – that’s the level the crow needs to be able to reach the water.
2. Measure the height of the water in the jar and record it.
3. One by one, add 6 stones to the water, recording the height of the water after each addition.
4. Stop and make a prediction. How many more does he need to add?

Analysis:

Open the Thirsty Crow applet and follow the directions. (I have pre-loaded it for this presentation, but the full directions are below.)

 

Make Your Own Applet:

We will be using free, online software, called GeoGebra to do our analysis. Click on Free Software and choose your platform. Download the appropriate program.

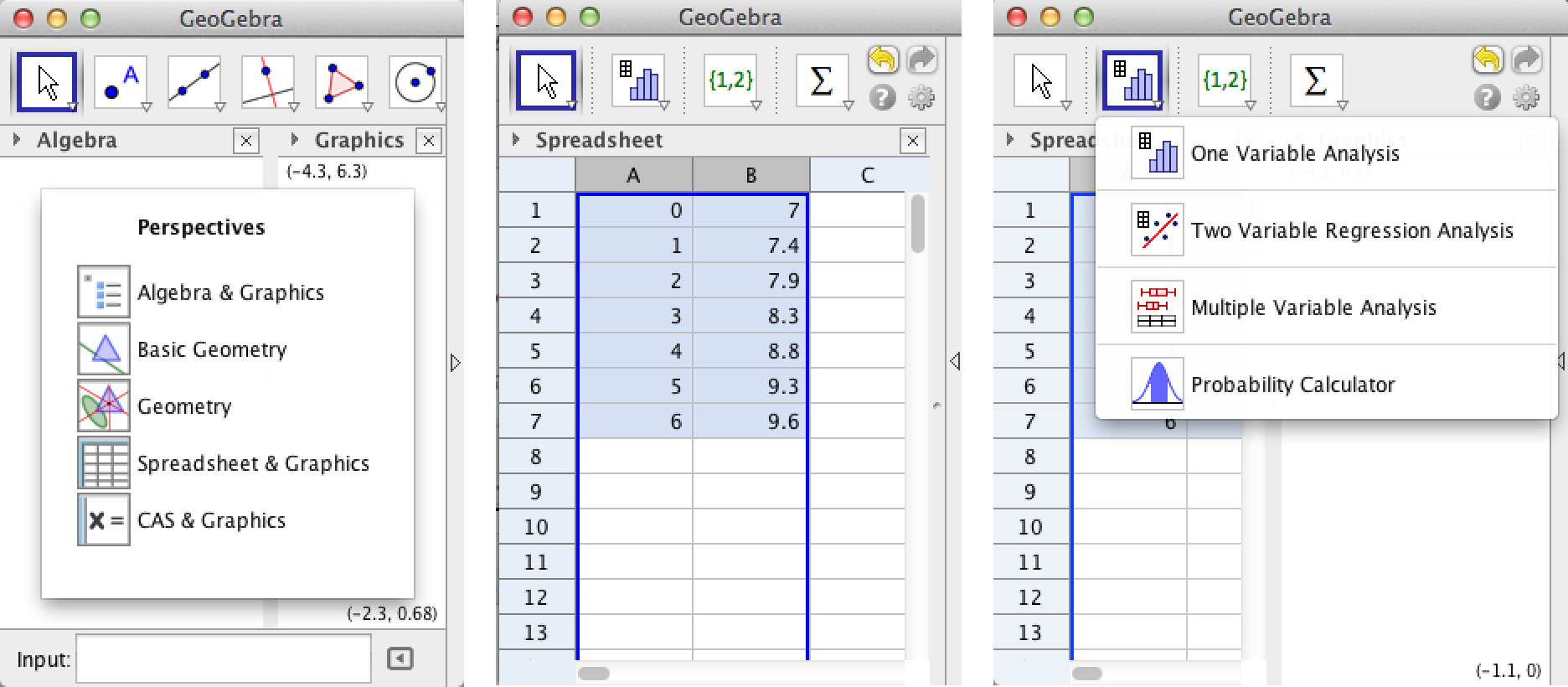
Open the program and choose “Spreadsheets and Graphics” from the Perspectives window.

Build your lists in columns A and B.

Highlight the columns and click on the little arrow in the bottom corner of the second icon from the left.

Choose Two Variable Regression Analysis.

Choose Analyze. Choose Linear from the “Regression Model” menu.

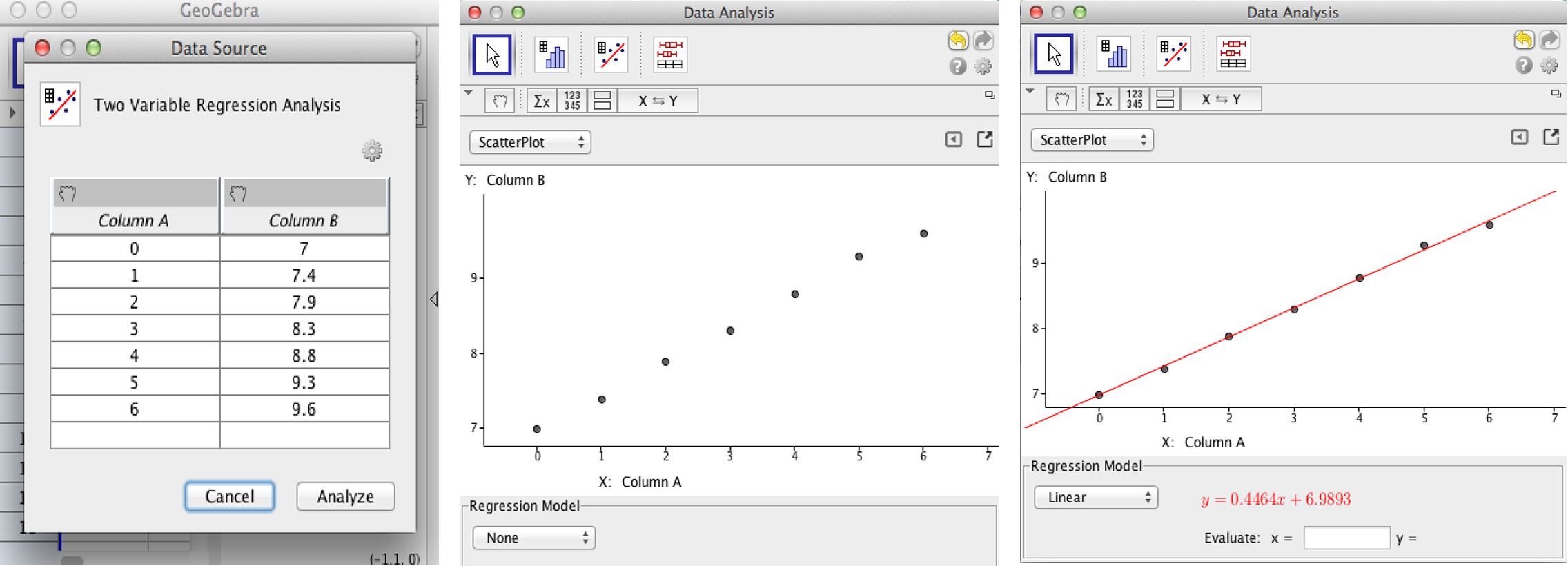
Interpretation:

The equation I got that best fits my data is y=0.4464x + 6.9893.

What do those numbers mean in terms of the situation?

How many more stones must she add?

Extension:

What could change in the problem?

How would that change the equation and graph?